Probability for randomize algorithm
Experiments
Sample Space
Event
Random variable
Expectation
Linearity of expectation
Experiments
Experiments are experiments or actions under the same circumstance. To roll a dice is experiments.
Sample Space
Sample space is that all possibilities of experiments. It is denoted by S = {1, 2, 3, 4, 5, 6}.
Event
Event is outcome of experiments under the certain situation. Event is grouped depending on certain situation by using A, B, C and represented by n(A), n(B), n(C). If you want to check the probability of getting number 3 and 6 by rolling dice, you can denote the event (not probability) like A = {3, 6} and n(A) = 2. The probability of event A is happened is denoted P(A) = n(A) / S which is P(A) = 2 / 6. S is sample space of rolling a dice which is 6.
Random variable
Random variable is that the variable contains random outcome. In programming world, var i = Math.random() or subarray passed into first recursive call. In real world, it could be the outcome of a rolling dice.
Probability
Probability should be expressed 0 <= n <=1, which means 0% <= n <= 100%. Pr(A) = 0.5 is A happens with 50% probability.
- Pr(S) = 1
- 0 <= Pr(A) <= 1
- When A AND B = {}. Pr(A U B) = Pr(A) + Pr(B)
Pr(X = Ck) means the probability that random variable X is equal to Ck.
Expectation
Expectation is the outcome of . It is denoted by using µ or E(x) or µ(x) and x is random variable so that means "Expectation" of random variable. The expectation of random variable of rolling a dice S = {1, 2, 3, 4, 5, 6} is E(X) = 1 + 2 + 3 + 4 + 5 + 6 / 6 = 3.5.
Expectation can be denoted below.
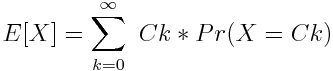
- E[X] means expectation of random variable X
- Pr(X=Ck) means the probability of X is equal to Ck
- Ck is the value which is result of random variable. C0, C1, C2, C3....Ck. k is index and Ck means not C*k but just getting value C[0], C[1], C[k]. In the case of rolling a dice, it will be C0 = 1, C1 = 2, C2 = 3, C3 = 4, C4= 5, C5=6
Back to rolling a 6 dimension dice case, we are doing this math below.

C[0], C[1] C[2], C[3], C[4], C[5] = 1, 2, 3, 4, 5, 6
Pr(X = Ck) is 1 / 6 because it is probability of getting one value out of 6 dimensions.
Equal to...

so E[X] = 1 + 2 + 3 + 4 + 5 + 6 / 6 = 3.5.
Indicator Random variable
An indicator random variable is a special kind of random variable associated with the occurence of an event.
If you check random events whether element i and j are compared or not, indicator random variable can be expressed like below.
Linearity of expectation
Linearity of expectation is theorem describe that sum of expectations are same as expectations of sum.
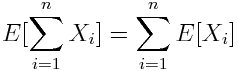
For example, in the case of rolling 2 dices, the expectation could be represented in two way and both outcomes are same.
http://dopal.cs.uec.ac.jp/okamotoy/lect/2016/dme/term08.pdf (JP)
https://mathtrain.jp/expectation (JP)
Consider a group of n people. Assume that each person's birthday is drawn uniformly at random from the 365 possibilities. What is the smallest value of such that the expected number of pairs of distinct people with the same birthday is at least one?
https://math.stackexchange.com/questions/2140681/birthday-problem-among-k-people
Let 0 < α < 0.5 be some constant (independent of the input array length n). Recall the Partition subroutine employed by the QuickSort algorithm, as explained in lecture. What is the probability that, with a randomly chosen pivot element, the Partition subroutine produces a split in which the size of the smaller of the two subarrays is ≥α times the size of the original array?
- n is the size of input array.
α is
0 < α < 0.5 is equal to 0 < n * α < n * 0.5, which means smaller than half size of the array.
https://stackoverflow.com/questions/25477735/probabilty-based-on-quicksort-partition
Now assume that you achieve the approximately balanced splits above in every recursive call --- that is, assume that whenever a recursive call is given an array of length kk, then each of its two recursive calls is passed a subarray with length between \alpha kαk and (1-\alpha)k(1−α)k (where \alphaα is a fixed constant strictly between 0 and .5.5). How many recursive calls can occur before you hit the base case? Equivalently, which levels of the recursion tree can contain leaves? Express your answer as a range of possible numbers dd, from the minimum to the maximum number of recursive calls that might be needed.
Let X_1,X_2,X_3X 1 ,X 2 ,X 3 denote the outcomes of three rolls of a six-sided die. (I.e., each X_iX i is uniformly distributed among {1,2,3,4,5,6}1,2,3,4,5,6, and by assumption they are independent.) Let YY denote the product of X_1X 1 and X_2X 2 and ZZ the product of X_2X 2 and X_3.X 3 . Which of the following statements is correct?

