Algorithm
- Time and space complexity
- Recursion vs loop
Divide and conquer
Dynamic programming
Greedy
Backtracking
Sorting algorithm
Searching algorithm
Time Complexity
Time complexity is the concept to major the time of your algorithm according to N size of input and is represented by using Big O notation. Time complexity is illustrated by polynomial expression like 2n² + n however constant and smaller time complexity will be able to be ignored for the sake of comparison to other time complexity of algorithm. For example,
f(n) = 2n² + n + 1
could be simplified to
f(n) = n²
| Time | ||
|---|---|---|
| O(n**2) | Quadratic time | Nested loop |
| O(n * log n) | Quasilinear time | N times iterated with log(n) time |
| O(n) | Linear time | Iterate over all elements once |
| O(log n) | Logarithmic time | Divide the group of elements into half each loop |
| O(1) | Constant time | No matter how input size is big, one time |
| Notation | Condition | |
|---|---|---|
| Ο Notation | upper bound of an algorithm's running time. | f(n) = c * g(n) AND c * g(n) >= 0 n⁰ >= 1 |
| Ω Notation | lower bound of an algorithm's running time | |
| θ Notation | both the lower bound and the upper bound of an algorithm's running time (tight) |
Big O (upper bound)
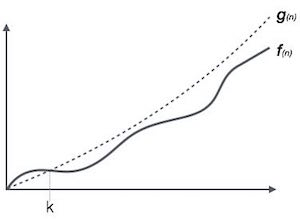
Omega (lower bound)
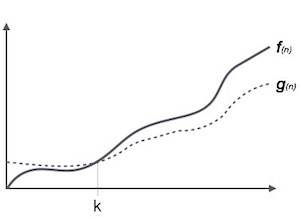
Theta (Tight bound)

Suppose we have this function and time complexity.
f(n) = 2n² + n + 1
According to this order,
1 < log n < n < n log n < n² < n³ < .... < 2ⁿ < nⁿ
The function can be explained by using Omega notation and Big O notation.
Omega
f(n) = Ω(1)
f(n) = Ω(logn)
f(n) = Ω(n)
f(n) = Ω(n log n)
Big O
f(n) = O(n²)
f(n) = O(n³)
f(n) = O(2ⁿ)
https://hackernoon.com/what-does-the-time-complexity-o-log-n-actually-mean-45f94bb5bfbf
https://cs.stackexchange.com/questions/192/how-to-come-up-with-the-runtime-of-algorithms
Mater Theorem
Calculating running time of recursion is hard so that we need to use master theorem to assume running time of recursion more accurately. These are two steps to calculate running time.
- Find out a, b, d, f(n) out of recurrence formula.
- Match the cases of master mind. Find out the relation between nᵈ and f(n) and match to a pattern out of 3.
1. What is a, b, d, f(n)?
Recursion function can represent accordingly.
T(n) = aT(n/b)+O(nᵈ)
a - number of recursive calls. (a>=1)
b - how many times do you divide elements, which is called shrinkage factor. If you split elements into 2 groups, b will be 2 such as merge sort. (b > 1)
O(nᵈ) - This represents outside of recursion.
2. The cases of mater method. (Find out relation between a, b, and d)

By using a, b, and d, we can find out three patterns such as T(n) = O(nᵈ log n), T(n) = Θ(nᵈ), T(n) = O(n ^(log𝖻ª)).
a is rate of subproblem profiler. (RSP)
bᵈ is rate of work shrinkage per subproblem (RWS)
The cases of master method compares RSP and RWS and check if it is larger, smaller, or equal.
- If RSP is equal to RWS, the amount of work is same at every recursion level j.
- If RSP < RWS, then the amount of work is decreasing with the recursion level j.
- If RSP > RWS, then the amount of work is increasing with the recursion level j.
Ex1:) Merge Sort - T(n) = 2T(n/2)+O(n)
a: 2 => 2 functions are called recursively
b: 2 => Elements are divide into 2 groups each time.
f(n): O(n) running computation besides recursive function
d: 1
function mergeSort (arr) {
if (arr.length === 1) {
return arr
}
/*
Merge sort divides elements right and left, which is 2 groups so that b = 2 (n/2)
*/
const middle = Math.floor(arr.length / 2)
const left = arr.slice(0, middle)
const right = arr.slice(middle)
/*
This function is called merge sort at 2 times so a = 2
*/
return merge(
mergeSort(left),
mergeSort(right)
)
}
/*
This operation is O(n)
*/
function merge (left, right) {
let result = []
let indexLeft = 0
let indexRight = 0
while (indexLeft < left.length && indexRight < right.length) {
if (left[indexLeft] < right[indexRight]) {
result.push(left[indexLeft])
indexLeft++
} else {
result.push(right[indexRight])
indexRight++
}
}
return result.concat(left.slice(indexLeft)).concat(right.slice(indexRight))
}
2 = 2¹ matches case 1 (a = bᵈ) so running time is O(𝘯¹ log 𝘯)
Ex2:) T(n) = T(n/2)+O(n)
a: 1
b: 2
d: 0
function binarySearch(array,low,high,num) {
var mid;
if(low > high) {
return -1;
}
/*
split into 2 groups so that b = 2
*/
mid = Math.floor(low+(high-low)/2);
if (num == array[mid]) {
return mid;
}
/*
calls binarySearch() one time
*/
else if (num<array[mid]) {
return binarySearch(array,low,mid-1,num);
}
else {
return binarySearch(array,mid+1,high,num);
}
/*
No other computation so that O(n⁰) d = 0
*/
}
binarySearch([5,6,17,25,33,47,72,90,106],0,8,17);
1 = 2⁰ matches case 1 (a = bᵈ) so running time is O(𝑛⁰ log 𝑛) = O(log 𝑛)
Space Complexity
Space complexity represents the additional memory space used during algorithm execution. Big-O notation can be also applied.
| Space | |
|---|---|
| O(n) | Need space as much as the number of elements. Typically on recursion. |
| O(log n) | Need some space at stack during recursion |
| O(1) | Does not depend on the size of the input. If you just need several variables or constants, it will be constant |
https://www.quora.com/How-do-we-calculate-space-complexity
https://stackoverflow.com/questions/12573330/why-does-quicksort-use-ologn-extra-space
Recursion vs Loop
In the point of view of time and space complexity, recursion and loop are different. Basically, recursion takes more space than loop. Time complexity won't be changed that much in theory. However, function calls are expensive comparing to jumping inside a function so recursion is not effective. Recursion makes the solution more simple but not good for production in most case.
https://stackoverflow.com/questions/9386375/efficiency-recursion-vs-loop
Recursion
https://www.tutorialspoint.com/analysis_of_algorithm/index.asp
Divide and conquer
- Divide a problem into subproblems
- Conquer via recursion call
- Combine results of the subproblems into one problem
Dynamic Programming
Dynamic Programming is the way to implement algorithm in efficient by storing the solution to subproblem. This has to satisfy the following conditions.
- Break the problem into sub problems
- Store and re use solution to sub problem which is solved previously. (Memoize)
By re-using solution, the time of the computation will be shorter. For example, suppose you try to calculate fibonacci numbers, the time complexity is O(n**2).
Memoize Basic Implementation
var memoize = function(func) {
const cache = {};
return (...args) => {
const key = JSON.stringify(args);
// IF cache does not have key, THEN call function
return key in cache ? cache[key] : (cache[key] = func(...args));
}
}
fibonacci = memoize(fibonacci);
In this example, it uses hi order pattern and return a function from memoize function and now fibonacci function is wrapped by memoize function.
Example
Factorial
Knapsack Problem
https://people.eecs.berkeley.edu/~vazirani/algorithms/chap6.pdf
https://stackoverflow.com/questions/35026477/big-o-of-fibonacci-with-memoization
https://medium.freecodecamp.org/understanding-memoize-in-javascript-51d07d19430e
http://www.jstips.co/en/javascript/speed-up-recursive-functions-with-memoization/
https://www.youtube.com/watch?v=xOlhR_2QCXY
Greedy algorithm
Greedy algorithm is one of the patterns of algorithm. It chooses from the closest or biggest element to far most or smallest element. This is why it is called "greedy". For example, if the program needs to find combination of least amount of bills from $120, it will start choosing from $100 at first and $20 after. You could start from $5 * 24 and $ $10 * 12 but greedy does start from largest bill, which often has minimum number of elements.
Backtracking
![]()
Sort Algorithm

Bubble sort
Bubble sort is a simple sorting algorithm. It iterates whole elements and switches the element and the next element if the element is bigger than next element. It requires a variable to store a value to be switched temporarily so the space complexity is O(1).
Selection Sort
Insertion Sort
Quick Sort
Quick sort uses partition algorithm (It does not have combine phase unlike merge sort).
Divide: First rearrange then split the array into 2 subarrays using pivot. Pivot can be anything like first element, last element, or middle. But after rearranging an array, pivot needs to be replaced on the middle and split the array into 2 subarray.
Conquer: Quick sort the resulting subarrays recursively.
Merge Sort
- Divide: Split the array into 2 subarrays
- Conquer: Merge sort the resulting subarrays recursively
- Combine: Merge the two sorted subarrays into a single sorted list
Heap Sort
brute-force search (exhaustive search)
In computer science, search or exhaustive search, also known as generate and test, is a very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's statement.
https://en.wikipedia.org/wiki/List_of_algorithms
https://www.coursera.org/learn/algorithms-part1/
https://github.com/bearpaw/Algorithms-Part-I/tree/master/A1_Percolation
